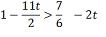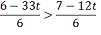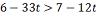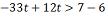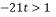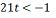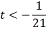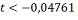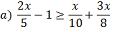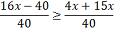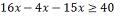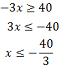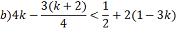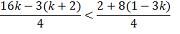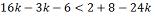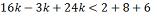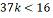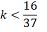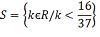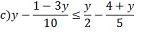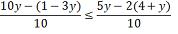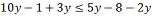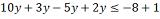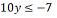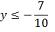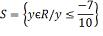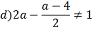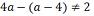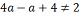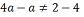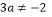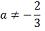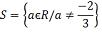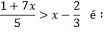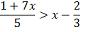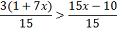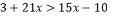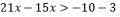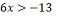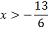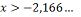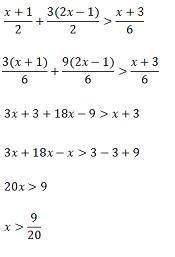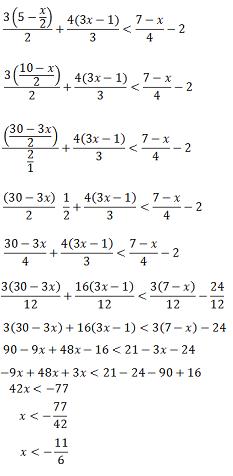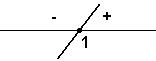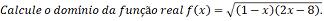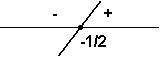Inequação do 1º grau

Inequações do 1º grau são aquelas que podem ser representadas sob a forma ax + b > 0 ( ou com as representações  ≥ , < , ≤ , ou ≠) em que a e b são constantes reais, com a ≠ 0, e x  é variável. A resolução desse tipo de inequação é fundamentada nas propriedades das desigualdades descritas a seguir:

1) Adicionando um mesmo número a ambos os membros de uma inequação, ou subtraindo um mesmo número de ambos os membros, a desigualdade se mantém.

2) Dividindo ou multiplicando ambos os membros de uma inequação por um mesmo número positivo, a desigualdade se mantém.

3) Dividindo ou multiplicando por um mesmo número negativo ambos os membros de uma inequação do tipo > , ≥ , < ou ≤ , a desigualdade inverte o sentido.

É fácil perceber que a resolução de uma inequação do 1º grau baseia-se nos mesmos princípios da resolução de uma equação do 1º grau atentando-se ao item 3) acima que diferencia.  Uma inequação do 1º grau é resolvida da mesma forma que se resolve uma equação do 1º grau, só que quando o x é negativo no final da resolução multiplica-se ambos os membros da inequação por (-1) e aí o sentido se inverte, se é  > fica  <, se é < fica >, se é ≤ fica ≥ e se é ≥ fica ≤.

Considerando como universo o conjunto dos números naturais, determine o conjunto solução da inequação:

5x – 8 < 3x + 12

5x – 3x < 12 + 8

2x < 20

 x < 20/2

x < 10

Assim o conjunto solução da inequação é:

S = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

Se, o universo do exercício anterior fosse o conjunto dos números reais, qual seria o conjunto solução da inequação?

Resolução:

Não é possível explicitar, um a um, todos os números reais menores que 10. Por isso, representa-se o conjunto solução S simplesmente por

S = {x/x є R/ x < 10}

Determine o maior número inteiro t que satisfaz a desigualdade:

O maior número inteiro que satisfaz essa desigualdade é o -1

Considerando o universo dos números inteiros, determine o conjunto solução das inequações:

a) 9x – 5(3 – 2x) > 7x + 9

    9x – 15 + 10x > 7x + 9

19x – 7x > 9 + 15

         12x > 24

              X > 24/12

              X > 2

S = {3, 4, 5, 6, ...}

b) 4y – 5 < 2(y + 3) + 5y

    4y – 5 < 2y + 6 + 5y

     4y – 5 < 7y + 6

     4y – 7y < 6 + 5

          -3y < 11

          3y  > -11

             Y > -11/3

             Y > -3,666…

S = {-3,-2,-1,0, 1, 2, 3…}

c) 6t – (5t + 8) ≤ 1 – 2(5 – t)

    6t – 5t – 8 ≤ 1 – 10 + 2t

    6t – 5t – 2t ≤ 1 – 10 + 8

                     -t ≤ -1

                      t  ≥ 1

S = {1, 2, 3, 4, 5, …}

Resolver as inequações no universo R:

S = {x є R/ x ≤ -40/3}

O menor número inteiro que satisfaz a inequação

a)-3                            c)-1                 e)1

b)-2                            d)0

Alternativa correta b(-2)

Resolver no universo R as inequações:

a) -3(2x – 5) > 1 – 6x

     -6x + 30 > 1 – 6x

      -6x + 6x > 1 – 30

                0x > -29

  S = R (qualquer número multiplicado por zero é igual a zero e zero é maior que -29)

b) -3(2x – 5) < 1 – 6x

     -6x + 15 < 1 – 6x

     -6x + 6x < 1 – 15

              0x < -14

S = Ø (qualquer número multiplicado por zero é igual a zero e zero é maior que -14)

Resolver a inequação:

Resolver a inequação:

Resolver o sistema:

4x – 3 < 2x + 5

X + 2 > 2x – 6

Resolve-se cada sentença isoladamente

4x – 3 < 2x + 5                                        x + 2 > 2x – 6

4x – 2x < 5 + 3                                        x – 2x > -6 - 2

2x < 8                                                         -x > -8

  x < 8/2                                                       x < 8

  x < 4

A intersecção desses conjuntos é a solução do sistema

Gráfico

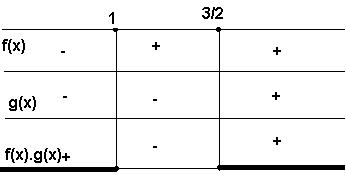
S = { x/x < 4}

Inequação-produto do 1º grau

Dadas as funções f(x) e g(x), chamamos de inequação-produto toda inequação que pode assumir uma das seguintes formas:

f(x).g(x) > 0               f(x).g(x) ≥ 0                f(x).g(x) < 0               f(x).g(x) ≤ 0

Oservação: a forma da inequação pode ser estendida para mais de duas funções.

Exemplos:

(x – 1)(2x – 3)(x + 1) < 0                              (x – 2)(-2x + 1)(4 – x) ≤ 0

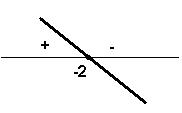
Para resolver inequações-produto, primeiro estudamos o sinal de cada função que compõe o produto e, então, determinamos o sinal do produto.

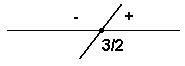
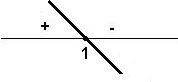
Acompanhe o procedimento nos exercícios resolvidos.

Resolva  em R a inequação (x – 1)(2x – 3) ≥ 0

Solução:

f(x) = x - 1  e   g(x) = 2x – 3

f(x) = 0 → x – 1 = 0 → x = 1 ( zero da função)

g(x) = 0 → 2x – 3 = 0 → 2x = 3 → x = 3/2

Como a = 2 > 0, vem:

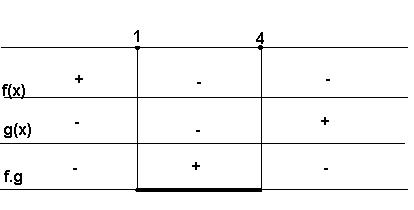
Quadro-produto

Logo:

S = {x є R/ x ≤ 1 ou x ≥ 3/2}

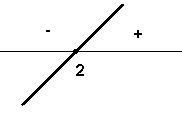
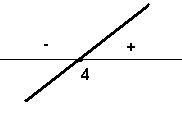
Resolva em R a inequação (x – 2)(-2x – 4)(x – 4) ≤ 0

Solução:

f(x) = x – 2, g(x) = -2x – 4 e h(x) = x – 4

f(x) = 0 → x – 2 = 0 → x = 2 (zero da função)

Como a = 1 > 0, vem:

g(x) = 0 → -2x – 4 = 0 →2x = -4→ x = -2(zero da função)

Como a = -2 < 0, vem:

h(x) = 0 → x – 4 = 0 →x = 4(zero da função)

Como a = 1 > 0, vem:

Quadro-produto

S = {x є R/-2 ≤ x ≤ 2 ou x ≥ 4}

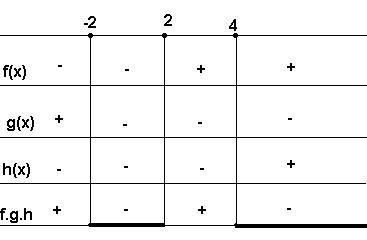
Solução:

Para que f seja real devemos ter:

(1 – x)(2x – 8) ≥ 0

1 – x = 0→x = 1

Como a = -1 < 0, temos:

2x – 8 = 0 → 2x = 8 → 2x = 8 → x = 8/2 = 4

Como a = 2 > 0, temos:

Quadro-produto:

Logo,D(f) = { x є R/  1 ≤ x ≤ 4}

Resolva as inequações em R:

a)(x – 1)(2x + 1) > 0

    x – 1 = 0 → x = 1

    Como a = 1 > 0, temos:

    2x + 1 = 0 → 2x = -1 → x = -1/2

    Como a = 2 > 0, temos:

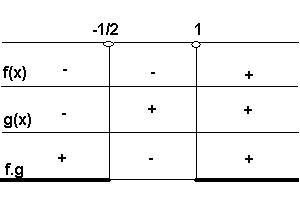
    Logo:

S = {x є R/ x < -1/2 ou x > 1}