|
Equação do 2º grau
Toda equação da forma
ax² + bx + c = 0, em que a, b e c são números reais com a ≠ 0, é chamada de equação do 2° grau. Quando b = 0 ou c = 0, tem-se uma equação do 2° grau incompleta.
A resolução de equações
incompletas do 2° grau:
Equações do tipo
ax² + bx = 0
1) Resolver em R a equação
x² - 4x = 0
Colocando o fator x
em evidência, obtemos:
x(x – 4) = 0
Quando o produto de
dois números reais é igual à zero, então pelo menos um dos fatores é igual a zero.
Portanto: x = 0 ou x – 4 = 0
x = 4
Logo as raízes são 0
e 4.
Verificação:
Para x = 0, temos: 0²
- 4.0 = 0 – 0 = 0 (V)
Para x = 4, temos: 4²
- 4.4 = 16 – 16 = 0 (V)
Portanto a solução está
correta.
2) Resolver em R a equação:
(2x + 5)² + 3x = 25
4x² + 20x + 25 +3x = 25
4x² + 23x = 0
x(4x + 23) = 0
x = 0
ou 4x + 23 = 0
4x = -23
x = -23/4
3) Resolver em R a equação:
4/2x – 3x = 2 + 2/x, sendo x
≠ 0
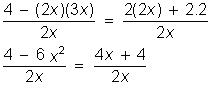
Multiplicando os dois membros da
equação por 2x, para eliminar os denominadores vem:
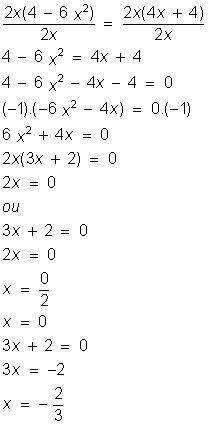
A partir do enunciado o número
zero foi excluído da solução dessa equação (x ≠ 0), então: x = -2/3 é solução única.
4) Resolver em R a equação:
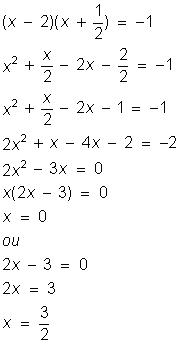
Equações do tipo ax² + c
= 0
5) Resolver em R a equação 2x² - 18 = 0
Adicionamos 18 aos dois membros
da equação:
2x² - 18 + 18 = 0 + 18
2x² = 18
Dividimos os dois membros da equação
por 2
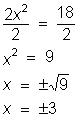
Então +3 e -3 são as raízes da
equação.
6) Resolver em R a equação:
2x² + 4 = 0
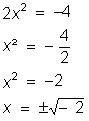
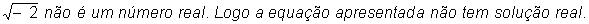
Equações do tipo ax² = 0
A equação do tipo ax² = 0 admite
uma única solução: x = 0
7) Resolver em R a equação 2x²
= 0
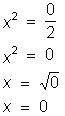
Exercícios:
Resolva as equações em R:
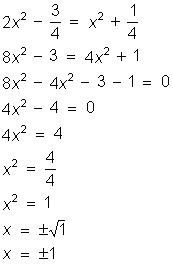
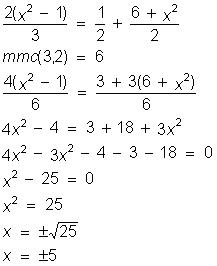
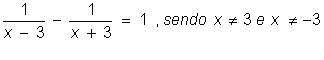
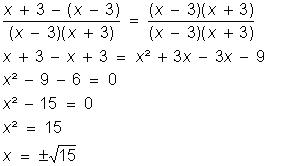
A resolução de equações completas
do 2º grau
Equações do tipo: ax² + bx + c
= 0
Qualquer equação do 2º grau pode
ser resolvida através da fórmula de Bháskara , o método usado anteriormente serve para facilitar a resolução de equações incompletas
em b e em c, principalmente as incompletas em b que são muito mais fáceis de serem resolvidas daquela forma, pois o uso da
fórmula de Bháskara naquele caso tornaria a solução mais complicada.
Demonstração da fórmula de Bháskara:
Dada a equação ax² + bx + c = 0
, multiplique os dois membros da equação por 4a:
(4a )(ax² + bx + c ) = (4a ) .
0
4a²x² + 4abx + 4ac = 0
4a²x² + 4abx = -4ac
Adicione b² aos dois membros da
equação:
4a²x² + 4abx + b² = -4ac + b²
Observe que o primeiro membro dessa
igualdade é um trinômio quadrado perfeito igual a (2ax + b)²
(2ax + b )² = b² - 4ac
Extraia a raiz quadrada dos dois
membros da igualdade:
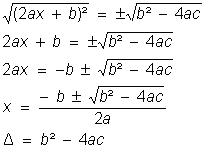
Resolver em R a equação 2x² - 10x + 12 = 0 :
Temos a = 2 , b = -10 e c = 12,
então:
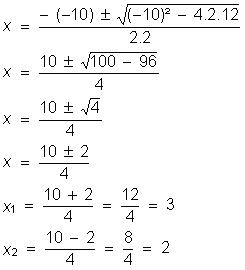
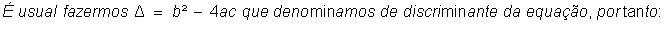
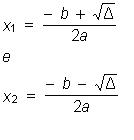
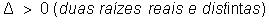
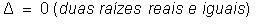
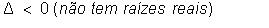
Relações entre os coeficientes
e as raízes
Relação de soma
Sendo x1 e x2 as
raízes da equação do 2º grau, desejamos obter a relação de soma em função dos coeficientes (a , b , c)
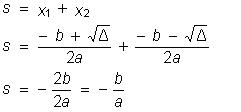
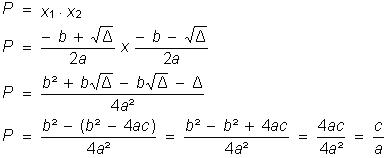
Fatoração do trinômio do 2º grau
Sendo r1 e r2 as raízes do trinômio do segundo grau ax² +bx +
c , temos que:
ax² + bx + c = a(x-r1)(x-r2)
Fatorar o trinômio do 2º grau
5x² - 3x – 2
Inicialmente determinamos as raízes
do trinômio. As raízes são os números que atribuídos a variável x anulam o trinômio, isto é, 5x² - 3x – 2 = 0
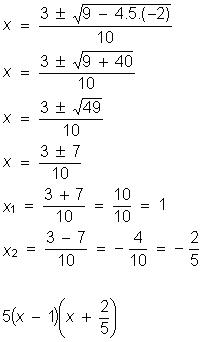
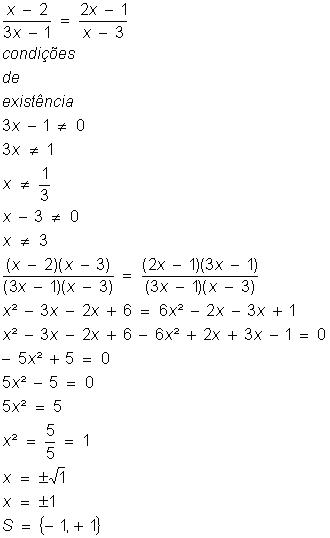
Obtenha as equações do 2º grau
conhecendo as raízes:
a) 2 e 3
(x – 2)(x – 3) = x² - 3x – 2x
+ 6 = x² - 5x + 6
x² - 5x + 6 = 0
b)-1 e -2
(x + 1)(x + 2) = x² + 2x + x + 2 = x² + 3x + 2
x² + 3x + 2 = 0
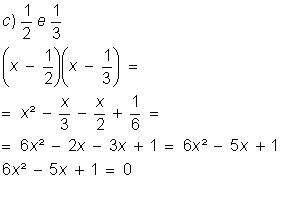
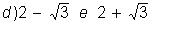
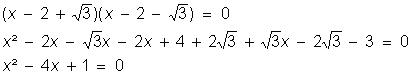
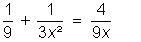
Condição de existência: x ≠
0
O mmc dentre os denominadores 3²
, 3x² e 3²x é o produto de todos os seus fatores, sendo que dentre fatores repetidos é escolhido o de maior expoente,isto
é:
mmc( 3²,3x²,3²x) = 3²x² = 9x²
Multiplicando ambos os membros
da equação por esse mmc,temos:
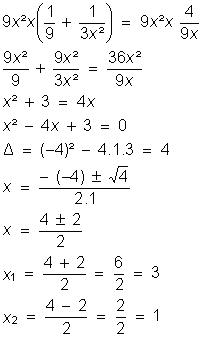
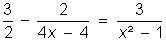
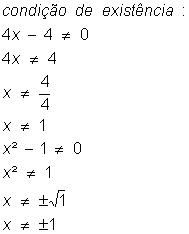
Para o calculo do mmc dentre os
denominadores, fatoramos cada um deles, obtendo:
2, 2²(x – 1) e (x + 1)(x
– 1). O mmc é o produto de todos os fatores desses polinômios, sendo que dentre fatores repetidos é escolhido o de maior
expoente, isto é:
mmc[2, 2²(x – 1), (x + 1)(x
– 1)] = 2²(x + 1)(x – 1)
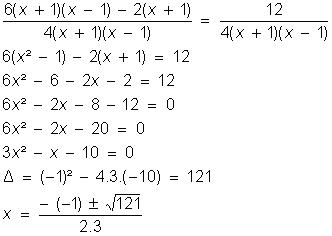
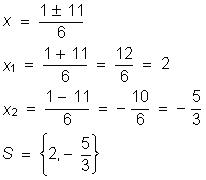
Exercícios resolvidos:
Resolva em R as equações:
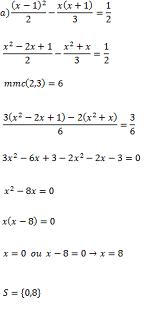
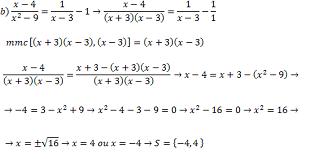
A área de um retângulo é igual a 440 m². Sabendo que a medida da base e a da altura desse
retângulo são números pares e consecutivos, determine seus valores.
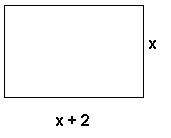
A = x(x + 2)
440 = x² + 2x
x² + 2x – 440 = 0

Resolva em R as seguintes equações:
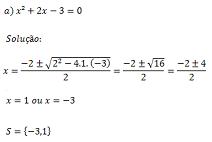
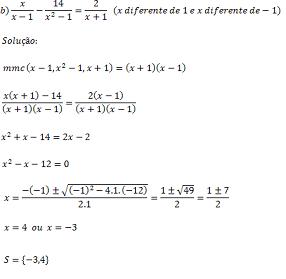
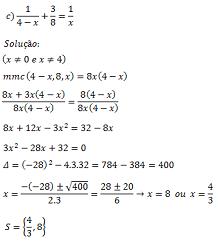
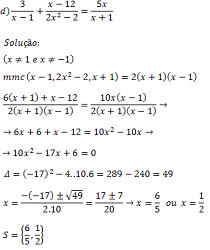
EXPRESSÕES NUMÉRICAS
EQUAÇÃO DO 1° GRAU
INEQUAÇÃO DO 1° GRAU
LOGARITMOS
PROGRESSÃO ARITMÉTICA E PROGRESSÃO GEOMÉTRICA
NÚMEROS COMPLEXOS
FUNÇÃO DO 2° GRAU
quimsigaud.blog.uol.com.br
|



