|
Triângulo retângulo é todo triângulo que
tem um ângulo reto. O triângulo ABC é retângulo em A e seus elementos são:
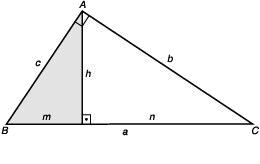
a: hipotenusa
b e c: catetos
h: altura relativa a hipotenusa
m e n: projeções ortogonais dos catetos
sobre a hipotenusa.
Relações métricas
Para um triângulo retângulo ABC podemos
estabelecer algumas relações entre as medidas de seus elementos:
- O quadrado de um cateto é igual ao produto
da hipotenusa pela projeção desse cateto sobre a hipotenusa.
b² = a.n
c² = a.m
- O produto dos catetos é igual ao produto
da hipotenusa pela altura relativa a hipotenusa.
b.c = a.h
- O quadrado da altura é igual ao produto
das projeções dos catetos sobre a hipotenusa.
h² = m.n
- O quadrado da hipotenusa é igual a soma
dos quadrados dos catetos.
a² = b² + c²
Essa relação é conhecida pelo nome de TEOREMA DE PITÁGORAS.
Exemplo:
Neste triângulo ABC, vamos calcular a,
h, m e n:
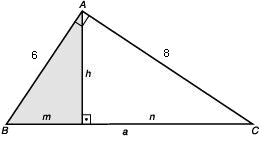
a² = b² + c² → a² = 6² + 8² →
a² = 100 → a = 10
b.c =
a.h → 8.6 = 10.h → h = 48/10 = 4,8
c² = a.m → 6² = 10.m → m =
36/10 = 3,6
b² = a.n → 8² = 10.n → n =
64/10 = 6,4
Determine os valores literais indicados
nas figuras:
a)
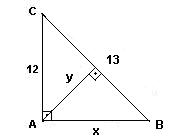
13² = 12² + x² 5.12
= 13.y
169 = 144 + x²
y = 60/13
x² = 25
x = 5
b)
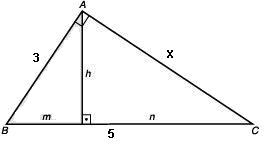
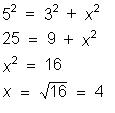
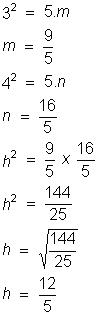

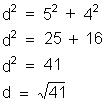
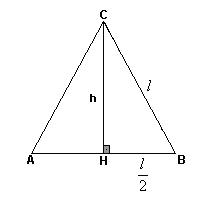
Determine a altura de um triângulo eqüilátero
de lado l.
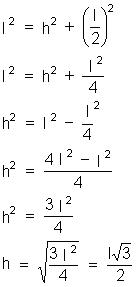
Determine x nas figuras.
a)
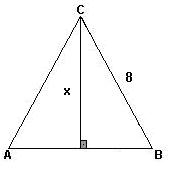
O triângulo ABC é eqüilátero.
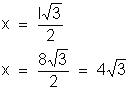
b)
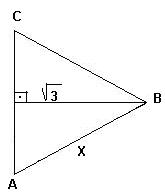
O triângulo ABC é eqüilátero.
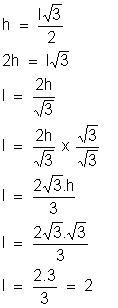
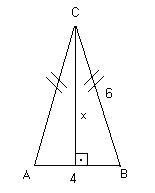
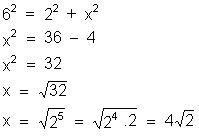
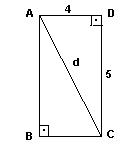
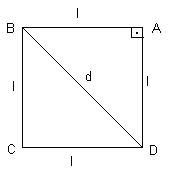
Determine a diagonal de um quadrado de
lado l.
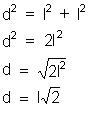

Razões trigonométricas
Considere um triângulo retângulo ABC. Podemos
definir:
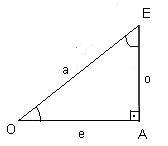
- Seno do ângulo agudo: razão entre o cateto
oposto ao ângulo e a hipotenusa do triângulo.
senÊ = e/a
senÔ = o/a
- Cosseno do ângulo agudo: razão entre
o cateto adjacente ao ângulo e a hipotenusa do triângulo.
cosÊ = o/a
cosÔ = e/a
- Tangente do ângulo agudo: razão entre
o cateto oposto ao ângulo e o cateto adjacente.
tgÊ = e/o
tgÔ = o/e
Observe: senÊ = cosÔ, senÔ = cosÊ e tgÊ = 1/tgÔ, sempre Ê + Ô = 90º
Exemplo:
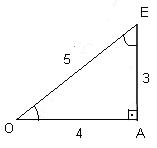
senÔ = 3/5 = 0,6
senÊ = 4/5 = 0,8
cosÔ = 4/5 = 0,8
cosÊ = 3/5 = 0,6
tgÔ = 3/4 = 0,75
tgÊ = 4/3 = 1,333....
Ângulos notáveis
Podemos determinar seno, cosseno e tangente
de alguns ângulos. Esses ângulos chamados de notáveis, são: 30°, 45° e 60°. A partir das definições de seno, cosseno e tangente,
vamos determinar esses valores para os ângulos notáveis. Considere um triângulo eqüilátero de lado l. Traçando a altura AM,
obtemos o triângulo retângulo AMC de ângulos agudos iguais a 30° e 60°. Aplicando as razões trigonométricas ao triângulo AMC
temos:
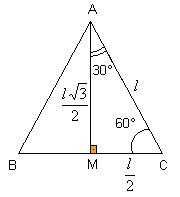

Para obter as razões trigonométricas do
ângulo de 45°, considere um quadrado de lado l. A diagonal divide o quadrado em dois triângulos retângulos isósceles.
No triângulo ABD, temos:
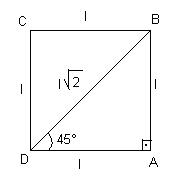
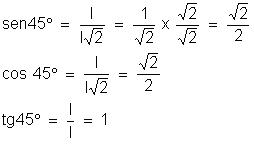
Observação: sen45° = cos45°
Resumindo temos a tabela:
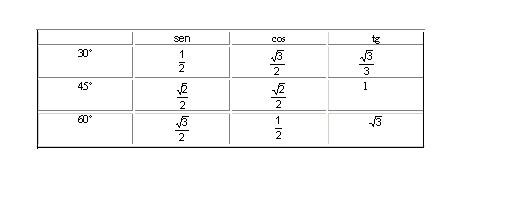
Exercícios resolvidos:
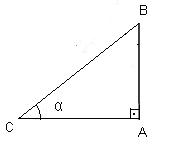
1) Calcule o perímetro
do triângulo retângulo ABC da figura, sabendo que o segmento BC é igual a 10 m e cos α = 3/5
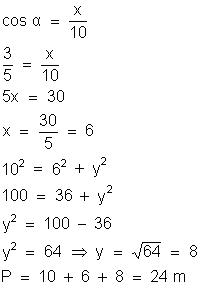
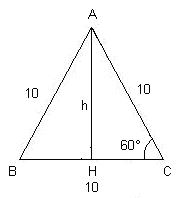
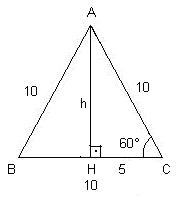
2) Calcule a altura de um triângulo eqüilátero
que tem 10 cm de lado.
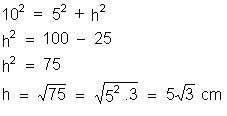
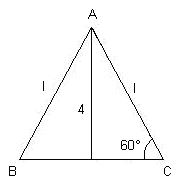
3) A altura de um triângulo eqüilátero
mede 4 cm. Calcule:
a) A medida do lado do triângulo
b) A área do triângulo
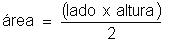
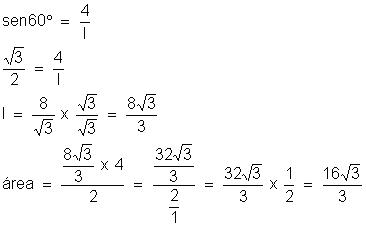
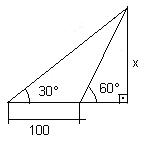
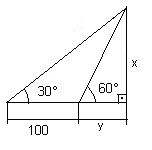
4) Calcule x indicado na figura
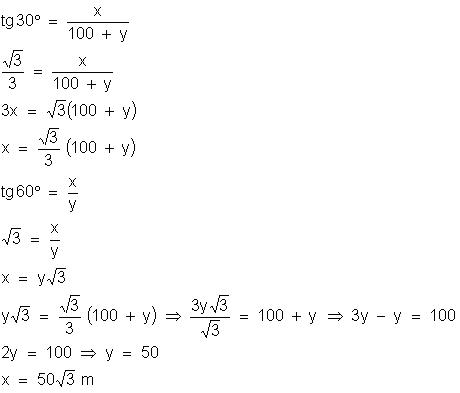
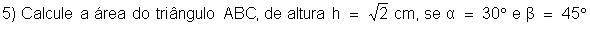
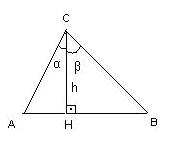
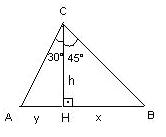
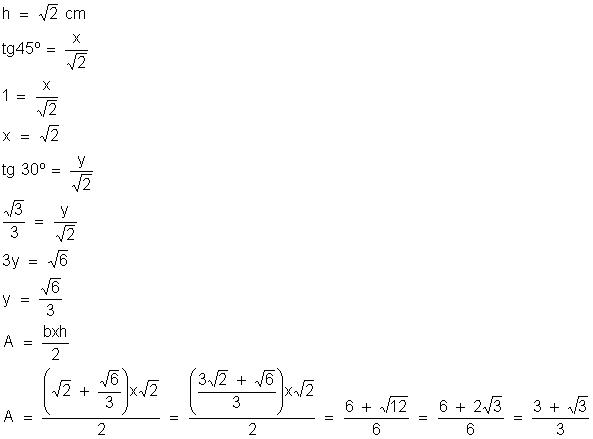
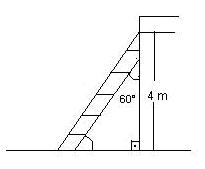
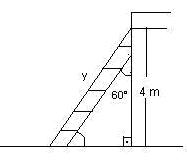
6) Uma escada apoiada em uma parede, num ponto distante 4 m dos solo, forma com essa parede um ângulo de 60°.
Qual é o comprimento da escada em metros?
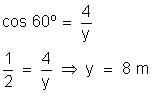
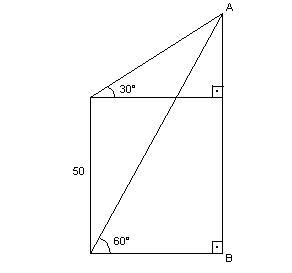
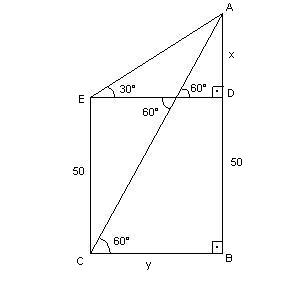
7) Na figura indicada
calcule AB.
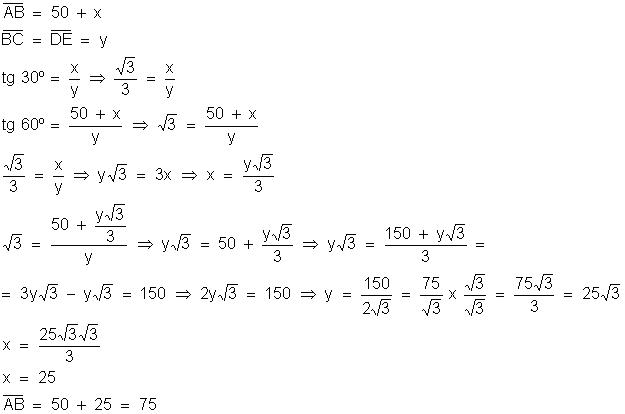
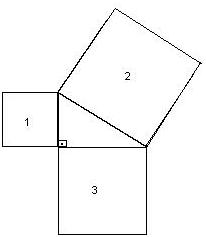
8) Observe na figura
os três quadrados identificados por 1,2 e 3. Se a área do quadrado 1 é 36cm² e a área do quadrado 2 é 100cm², qual é, em centímetros
quadrados, a área do quadrado 3 ?
A2 = A1
+ A3
100 = 36 + A2
A2 = 100
– 36 = 64cm²
9)As raízes da equação
x² - 14x + 48 = 0 expressam em centímetros as medidas dos catetos de um triângulo retângulo. Determine a medida da hipotenusa
e o perímetro desse triângulo.
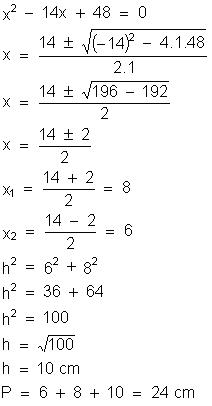
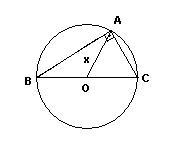
10) Sabe-se que, em
qualquer triângulo retângulo, a medida da mediana relativa à hipotenusa é igual à metade da medida da hipotenusa. Se um triângulo
retângulo tem catetos medindo 5cm e 2cm, calcule a representação decimal da medida da mediana relativa a hipotenusa nesse
triângulo.
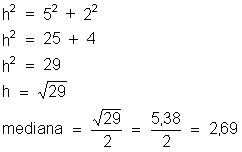
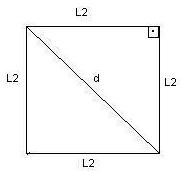
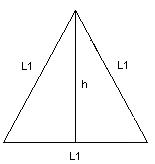
11) Um quadrado e um triângulo eqüilátero têm o mesmo perímetro.
Sendo h a medida da altura do triângulo e d a medida da diagonal do quadrado. Determine o valor da razão h/d.
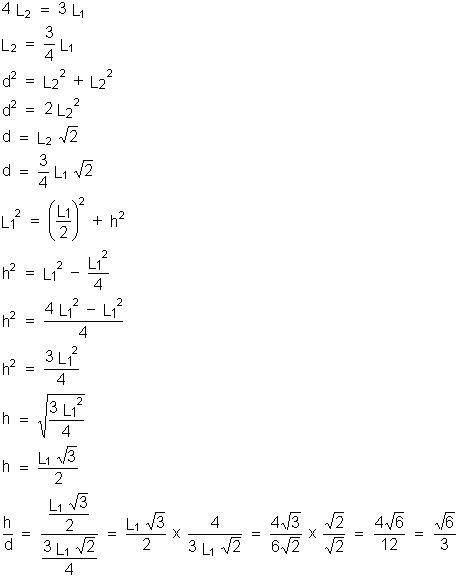
quimsigaud.blog.uol.com.br
Aulas particulares de matemática entrar em contato pelo e-mail
Professor: Joaquim Julio Marcondes Sigaud
Campos do Jordão - SP
|