|
As equações do primeiro grau são aquelas que podem ser representadas
sob a forma ax+b=0,em que a e b são constantes reais, com a diferente de 0, e x é a variável. A resolução desse tipo de equação
é fundamentada nas propriedades da igualdade descritas a seguir.
Adicionando um mesmo número a ambos os membros de uma equação, ou subtraindo um mesmo número de ambos
os membros, a igualdade se mantém.
Dividindo ou multiplicando ambos os membros de uma equação por um mesmo número não-nulo, a igualdade se mantém.
Exemplo:
Vejamos alguns exemplos:
Seja a equação:
Membros de uma equação
Numa equação a expressão situada à esquerda da igualdade é chamada
de 1º membro
da equação, e a expressão situada à direita da igualdade, de 2º membro da equação.
Exemplo: - 3x + 12 = 2x - 9
1º membro 2º membro
Cada uma das parcelas que compõem um membro de uma equação é chamada termo da equação.
4x – 9 = 1 – 2x
termos
Variável (ou incógnita) de uma equação:
Os elementos desconhecidos de uma equação são chamados de variáveis ou incógnitas.
Exemplos:
A equação x + 5 = 18 tem uma incógnita: x
A equação x – 3 = y + 2 tem duas incógnitas: x e y
A equação a² – 3b + c = 0 tem três incógnitas: a, b e c
Cada um dos valores que, colocados no lugar da incógnita, transformam a equação
em uma sentença verdadeira é chamado
de raiz da
equação.
Para verificarmos se um dado número é ou não raiz de uma equação, basta substituirmos a incógnita por esse número e observarmos
se a sentença obtida é ou não verdadeira.
1º exemplo: verificar se três é raiz de 5x – 3 = 2x + 6
2º exemplo: verificar se -2 é raiz de x² – 3x = x – 6
O princípio aditivo e o princípio multiplicativo servem para facilitar o entendimento da solução de
uma equação, mas para resolvê-la existe um método simples e prático que é o seguinte:
Resolver a equação 5x – 8 = 12 + x
Colocamos no primeiro membro os termos que apresentam variável, e no segundo membro os termos que
não apresentam variável. Os termos que mudam de membro tem os sinais trocados.
5x – 8 = 12 + x
5x – x = 12 + 8
Calculamos a somas algebricas de cada termo.
4.x = 20
Quando se passa de um membro para o outro usa-se a operação inversa, ou seja, o que está multiplicando
passa dividindo e o que está dividindo passa multiplicando. O que está adicinando passa subtraindo e o que está subtraindo
passa adicionando. O número 4 no primeiro membro está multiplicando o x então ele passará dividindo no segundo membro.
Exercícios resolvidos:
1) Resolver a equação:
2( x + 5 ) - 3( 5 – x ) = 5
Nesse tipo de equação, devemos inicialmente, retirar os parênteses, aplicando a propriedade
distributiva da multiplicação e a regra de eliminação de parênteses.
Para eliminar os denominadores multiplicamos todos os termos da equação pelo m.m.c. dos denominadores
|
 |
3) Resolução da equação:
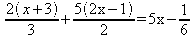
Nessa equação, inicialmente reduzimos todas as frações ao mesmo denominador,
e a seguir cancelamos esses denominadores
m.m.c ( 3, 2, 6 ) = 6
3, 2, 6 2
3, 1, 3 3
1, 1, 1 2 . 3 = 6
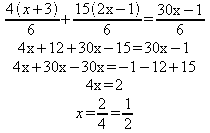
4) Resolver a equação:
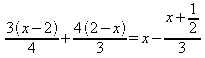
m.m.c ( 2, 3, 4 ) = 12
Efetuando as multiplicações:
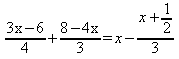
Multiplicando os dois membros da equação pelo m.m.c dos
denominadores, que é 12, vem:
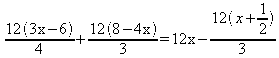
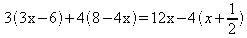
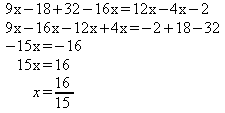
Resolvendo a mesma equação pelo método da eliminação dos denominadores:
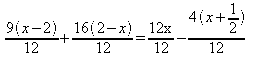
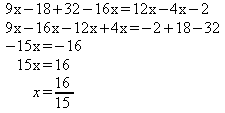
5) Resolver a equação:
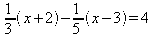
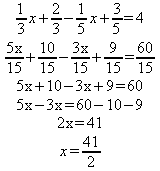
6) Resolver a equação:
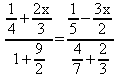
m.m.c ( 2, 3, 4, 5, 7 ) = 420
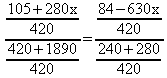
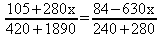
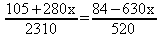
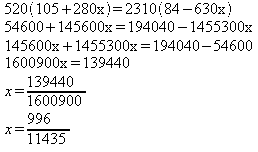
7) Quando o número x na equação ( k – 3
).x + ( 2k – 5 ).4 + 4k = 0 vale 3, qual será o valor de K?
( k – 3 ).3 + ( 2k – 5 ).4 + 4k = 0
3k – 9 + 8k – 20 + 4k = 0
3k + 8k + 4k = 9 + 20
15k = 29
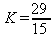
8) De o conjunto solução
das equações literais do primeiro grau ( em R )
a) ax + bx + c = 2a + 2b + c
ax + bx = 2a + 2b + c – c
x( a + b ) = 2a + 2b
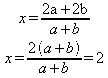
se a ≠
-b e b ≠
-a
b) ( a + x )² = ( a + 3 + x )( a – 2 + x )
a² + 2ax + x² = a² – 2a + ax + 3a – 6 + 3x + ax
– 2x + x²
2ax + x² – ax – 3x – ax + 2x – x² =
- a² + a² – 2a + 3a – 6
x(2a – a – 3 – a + 2) = a – 6
x(-1) = a – 6
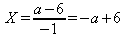
Equação sem solução
Às vezes, uma equação não tem solução para um certo universo de números. Nesse caso, dizemos que ela
é impossível
ou que
a solução é vazia.
Exemplo: resolver a equação.
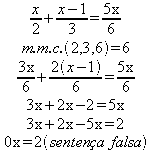
Não existe nenhum número que multiplicado por 0 que resulte em 2.
Equação com infinitas soluções
Há casos em que todos os números do universo considerado são raízes da equação. Dizemos que
ela tem infinitas
soluções.
Exemplo: resolver a equação
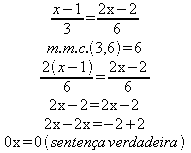
Como qualquer número multiplicado por zero é igual a zero, a equação tem infinitas
soluções.
INEQUAÇÃO DO 1° GRAU
EXPRESSÕES NUMÉRICAS
PRODUTOS NOTÁVEIS
EQUAÇÃO DO 2° GRAU
LOGARITMOS
PROGRESSÃO ARITMÉTICA E PROGRESSÃO GEOMÉTRICA
TRIÂNGULO RETÂNGULO
NÚMEROS COMPLEXOS
FUNÇÃO DO 2º GRAU
quimsigaud.blog.uol.com.br
|
|
|
