Função do 2º grau

A função f:R→R dada por f(x) = ax² + bx + c , com a,b e c reais e a ≠ 0, denomina-se função do 2º grau ou função quadrática.

Exemplos:

f(x) = x² - 4x – 3    ( a = 1, b = -4, c = -3)

f(x) = x² - 9      ( a = 1, b = 0, c = -9)

f(x) = 4x² + 2x – 3  ( a = 4, b = 2, c = -3)

f(x) = 6x²   ( a = 6, b = 0, c = 0)

f(x) = -2x² + 5x + 1 ( a = -2 , b = 5 , c = 1)

f(x) = -4x² + 2x  ( a = -4 , b = 2 , c = 0)

1) Dada a função f(x) = x² - 5x + 6, calcule:

a)f(1) = 1² - 5.1 + 6 = 1 – 5 + 6 = 2

b)f(-1) = (-1)² - 5.(-1) + 6 = 1 + 5 + 6 = 12

c)f(2) = 2² - 5.2 + 6 = 4 – 10 + 6 = 0

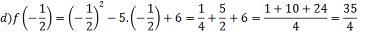
e)f(0) = 0² - 5.0 + 6 = 6

f)f(3) = 3² -5.3 + 6 = 9 – 15 + 6 = 0

2) Dada a função f(x) = 4x² - 1, calcule:

a)f(2) = 4.2² - 1 = 16 – 1 = 15

b)f(-1) = 4.(-1)² - 1 = 4 – 1 = 3

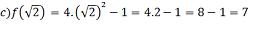
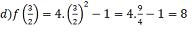
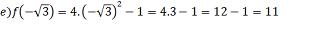
3) Dada a função f(x) = x² - 4x – 5, determine os valores de x para que se tenha:

a)f(x) = 7

x² - 4x – 5 = 7

x² - 4x – 5 – 7 = 0

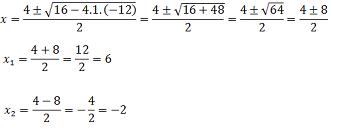
4) Dada a função f(x) = 2x² - 3x + 1, calcule:

a)f(-x) = ?

f(-x) = 2.(-x)² -3.(-x) + 1 = 2x² + 3x + 1

b)f(x + 1) = ?

f(x + 1) = 2.(x + 1)² - 3.(x + 1) + 1

=2.(x² + 2x + 1) – 3x – 3 + 1 = 2x² + x

c) a, para que f(a – 1) = 0

0 = 2.(a – 1)² - 3.(a – 1) + 1

0 = 2.(a² - 2a + 1) – 3a + 3 + 1

0 = 2a² -4a + 2 -3a +3 + 1

2a² - 7a + 6 = 0

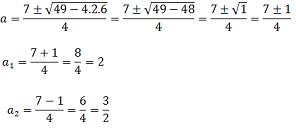
5) Dada as funções f(x) = 2x + 1 e g(x) = x² - 1 determine os valores reais de x  para que se tenha g(f(x)) = 0

g(2x + 1) = (2x + 1)² - 1 = 4x² + 4x + 1 – 1 = 4x² + 4x

4x² + 4x = 0

x² + x = 0

x(x + 1) = 0

x = 0

ou

x + 1 = 0

x = -1

6) Seja f(X) = ax² + bx + c . Sabendo que f(1) = 4, f(2) = 0 e f(3) = -2, calcule o produto a.b.c

f(1) = 4

a.1² + b.1 + c = 4

a + b + c = 4

f(2) = 0

a.2² + b.2 + c = 0

4a + 2b + c = 0

f(3) = -2

3².a + 3b + c = -2

9a + 3b + c = -2

a + b + c = 4

4a + 2b + c = 0

9a + 3b + c = -2

-4a – 4b – 4c = -16

4a + 2b + c  = 0

-2b -3c = -16

a + b + c = 4

9a + 3b + c = -2

-9a -9b – 9c = -36

-6b – 8c = -38

6b + 9c = 48

c = 10

-2b – 30 = -16

-2b = 30 – 16

-2b = 14

b = 14/-2 = -7

a – 7 + 10 = 4

a + 3 = 4

a = 4 – 3

a = 1

a.b.c = 1. -7.10 = -70

Construir o gráfico da função y = x² - 2x – 3

 x        y = x² - 2x – 3                    (x,y)

-2       y = (-2)² - 2.(-2) – 3 = 5    (-2,5)

-1       y = (-1)² - 2.(-1) – 3 = 0    (-1,0)

0        y = 0² - 2.0 – 3 = -3           (0,-3)

1      y = 1² - 2.1 – 3 = -4            (1,-4)

2      y = 2² - 2.2 – 3 = -3            (2,-3)

3      y = 3² - 2.3 – 3 = 0              (3,0)

4      y = 4² - 2.4 – 3 =5               (4,5)

Gráfico

Construir o gráfico da função y = 2x²

  x          y = 2x²                           (x,y)

-2          y = 2.(-2)² = 8                (-2,8)

-1          y = 2.(-1)² = 2                (-1,2)

0           y = 2.0² = 0                    (0,0)

1           y = 2.1² = 2                    (1,2)

2           y = 2.2² = 8                    (2,8)

Gráfico

Construir o gráfico da função y = -x² + 2x + 3

  x      y = -x² + 2x + 3                             (x,y)

-2      y = -(-2)² + 2.(-2) + 3 = -5            (-2,-5)

-1      y = -(-1)² + 2.(-1) + 3 = 0             (-1,0)

 0      y = -(0)² + 2.(0) + 3 = 3                (0,3)

1       y = -(1)² + 2.(1) + 3 = 4                 (1,4)

2       y = -(2)² + 2.(2) + 3 = 3                 (2,3)

3       y = -(3)² + 2.(3) + 3 =0                  (3,0)

4       y = -(4)² + 2.4 + 3 = -5                   (4,-5)

Gráfico

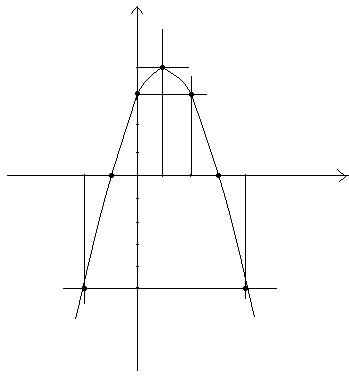
Construir o gráfico da função y = -x² + 2x – 4

  x          y = -x² +2x – 4                       (x,y)

-1          y = -(-1)² + 2.(-1) – 4 = -7     (-1,-7)

0              y = - (o)² + 2.0 – 4 = -4          (0,-4)

1           y = -(1)² + 2.1 – 4 = -3           (1,-3)

2           y = -(2)² + 2.2 – 4 = -4           (2,-4)

3           y = - (3)² + 2.3 – 4 = -7          (3,-7)

Gráfico

O gráfico de uma função do 2º grau ou quadrática é uma curva aberta chamada parábola.

Nos exemplos dados podemos observar que:

No 1º exemplo dado, f(x) = x² - 2x – 3,temos a = 1 > 0

No 2º exemplo dado, f(x) = 2x², temos a = 2 > 0

Em ambos, a parábola tem a concavidade voltada para cima.

No 3º exemplo dado, f(x) = -x² + 2x + 3, temos a = -1 < 0

No 4º exemplo dado, f(x) = -x² +2x – 4, temos a = -1 < 0

Em ambos, a parábola tem a concavidade voltada para baixo.

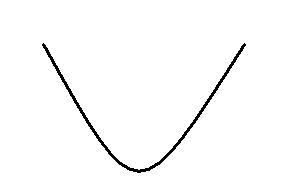
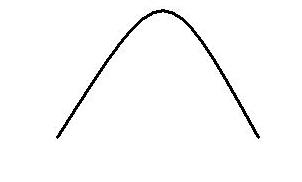
Se a <  0, a concavidade é voltada para baixo

Zeros de uma função quadrática

Os zeros ou raízes de uma função f(x) são os valores do domínio para os quais f(x) = 0.

Assim, os zeros ou raízes da função quadrática f(x) = ax² + bx + c são as raízes da equação do 2º grau ax² + bx + c = 0.

Por exemplo, para determinar as raízes da função f(x) = x² -7x + 6, fazemos:

f(x) = 0 → x² - 7x + 6 = 0

 equação do 2º grau

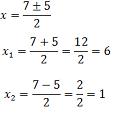
Então os números 1 e 6 são os zeros da função f(x) = x² - 7x + 6.

Você notou que, para determinar as raízes ou zeros da função quadrática tivemos que resolver uma equação do 2º grau. Vale a pena relembrar algo a respeito das raízes dessa equação. (vá no meu site de equação do 2º grau que é o quimsigaud.tripod.com/equacaodo2grau)

Para determinar os zeros ou raízes de uma função f(x) = ax² +bx + c, temos que analisar a equação ax² + bx + c = 0.

Se  Δ > 0, a função possui dois zeros reais distintos.

Se  Δ = 0, a função possui um zero real duplo.

Se  Δ < 0, a função não possui zeros reais.

Interpretação geométrica das raízes

Os zeros ou raízes de uma função são os valores de x tais que f(x) = 0. No plano cartesiano, são os pontos do gráfico da função que possuem ordenada nula.

Geometricamente, os zeros ou raízes de uma função polinomial do 2º grau são as abscissas dos pontos em que a parábola intercepta o eixo x.

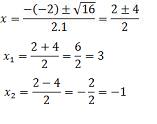
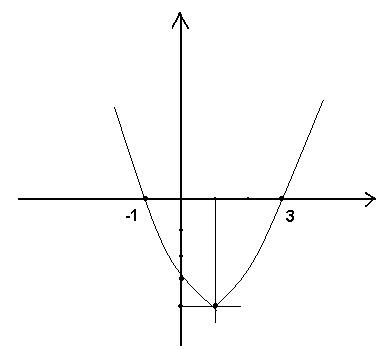
Como a função possui dois zeros reais diferentes, a parábola   intercepta o eixo x em dois pontos distintos: (-1,0) e (3,0).

Esboço do gráfico:

 f(x) = o → -x² +2x – 1 = 0

Δ = 2² - 4.(-1).(-1) = 4 – 4 = 0 ( a função possui um zero real duplo)
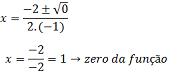